Las proposiciones conjuntivas están formadas por la unión de 2 proposiciones simples mediante la conjunción -"TAMBIÉN" - "ADEMÁS" - "PERO" - "SIN EMBARGO" - "COMO"; y también los signos de puntuación "," - "."
Ejemplo:
Da clic para seguir el vínculo:
Se le llama proposición disyuntiva a toda proposición simple que lleva como enlace el término: "O"
Estas proposiciones son:
Proposiciones disyuntivas Inclusivas. – son también llamadas débiles, son las que plantean 2 situaciones, pudiendo realizarse una y también la otra.
Ejemplo:
Santiago es la capital de Chile o Lima es la capital del Perú.
Proposiciones disyuntivas Exclusivas.- son también llamadas fuertes, son las que plantean 2 situaciones, de la cual solo una de ellas es posible y la otra no. Su conectivo lógico hace uso de dos “o” una al comienzo de la primera proposición y la otra como enlace a la segunda proposición.
Ejemplo:
O Lima es la capital de Perú o Lima es la capital de Chile.
Da clic para seguir el vínculo:
Son también llamadas débiles, son las que plantean 2 situaciones, pudiendo realizarse una y también la otra. Hace uso del conectivo lógico “o” que sirve para enlazar las dos proposiciones simples.
Ejemplo:
Santiago es la capital de Chile o Lima es la capital del Perú.
Da clic para seguir el vínculo:
son también llamadas fuertes, son las que plantean 2 situaciones, de la cual solo una de ellas es posible y la otra no. Su conectivo lógico hace uso de dos “o” una al comienzo de la primera proposición y la otra como enlace a la segunda proposición.
Ejemplo:
O Lima es la capital de Perú o Lima es la capital de Chile.
Da clic para seguir el vínculo:
Son también llamadas Inclusivas, son las que plantean 2 situaciones, pudiendo realizarse una y también la otra. Hace uso del conectivo lógico “o” que sirve para enlazar las dos proposiciones simples.
Ejemplo:
Santiago es la capital de Chile o Lima es la capital del Perú.
Da clic para seguir el vínculo:
son también llamadas Exclusivas, son las que plantean 2 situaciones, de la cual solo una de ellas es posible y la otra no. Su conectivo lógico hace uso de dos “o” una al comienzo de la primera proposición y la otra como enlace a la segunda proposición.
Ejemplo:
O Lima es la capital de Perú o Lima es la capital de Chile.
Da clic para seguir el vínculo:
Esta implicación se establece mediante un conectivo, dicho conectivo puede ser "SI. ENTONCES". De esta manera se puede entender que el enunciado hipotético resulta de colocar la palabra "si" antes de la primera proposición simple y la palabra "entonces" antes de la segunda proposición simple, por esta razón se llaman condicionales, enunciado implicativo o simplemente implicación.
Ejemplo:
Da clic para seguir el vínculo:
Se da cuando la operación de implicación está desordenada (en lenguaje natura! o científico). Es decir cuando primero está el consecuente y luego el antecedente.
Ejemplo:
Da clic para seguir el vínculo:
Esta implicación se establece mediante un conectivo, dicho conectivo puede ser "SI. ENTONCES". De esta manera se puede entender que el enunciado hipotético resulta de colocar la palabra "si" antes de la primera proposición simple y la palabra "entonces" antes de la segunda proposición simple, por esta razón se llaman condicionales, enunciado implicativo o simplemente implicación.
Ejemplo:
Da clic para seguir el vínculo:
Se da cuando la operación de implicación está desordenada (en lenguaje natura! o científico). Es decir cuando primero está el consecuente y luego el antecedente. Ejemplo:
Da clic para seguir el vínculo:
Esta implicación se establece mediante un conectivo, dicho conectivo puede ser "SI. ENTONCES". De esta manera se puede entender que el enunciado hipotético resulta de colocar la palabra "si" antes de la primera proposición simple y la palabra "entonces" antes de la segunda proposición simple, por esta razón se llaman condicionales, enunciado implicativo o simplemente implicación.
Ejemplo:
Da clic para seguir el vínculo:
Se da cuando la operación de implicación está desordenada (en lenguaje natura! o científico). Es decir cuando primero está el consecuente y luego el antecedente.
Ejemplo:
Da clic para seguir el vínculo:
Esta implicación se establece mediante un conectivo, dicho conectivo puede ser "SI. ENTONCES". De esta manera se puede entender que el enunciado hipotético resulta de colocar la palabra "si" antes de la primera proposición simple y la palabra "entonces" antes de la segunda proposición simple, por esta razón se llaman condicionales, enunciado implicativo o simplemente implicación.
Ejemplo:
Da clic para seguir el vínculo:
Se da cuando la operación de implicación está desordenada (en lenguaje natura! o científico). Es decir cuando primero está el consecuente y luego el antecedente.
Ejemplo:
Da clic para seguir el vínculo:
Se les llama proposiciones bicondicionales a aquellas que hacen uso del enlace "SI Y SOLO SI" para unir proposiciones simples.
Ejemplo:
Comerás si y solo si trabajas.
En este caso se puede observar cómo se entiende la doble implicación, por un lado se sabe que: "si comerá si trabaja; y por otro lado se entiende también que: si trabaja comerá".
Da clic para seguir el vínculo:
Las proposiciones negativas son llamadas también Inversores; son aquellas que cambian o invierten el sentido proposicional a partir de una proposición afirmativa que le dio origen.
Se presenta de dos modos, interna y externa, Ejemplo:
El perro no es un reptil. (negación interna).
Es mentira que José es abogado y Pedro es carpintero (negación externa).
Da clic para seguir el vínculo:
Las proposiciones negativas son llamadas también Inversores; son aquellas que cambian o invierten el sentido proposicional a partir de una proposición afirmativa que le dio origen.
Se presenta de dos modos, interna y externa, Ejemplo:
El perro no es un reptil. (negación interna).
Es mentira que José es abogado y Pedro es (negación externa).
Da clic para seguir el vínculo:
Las variables lógicas son símbolos que tienen por finalidad representar cualquier proposición simples, comúnmente se hace uso de las letras minúsculas: p, q, r, s, t,... etc.
Ejemplo:
p = El obrero carga
q = el jefe supervisa
r = el gerente administra
s = todos trabajan
Da clic para seguir el vínculo:
Las variables lógicas son símbolos que tienen por finalidad representar cualquier proposición simples, comúnmente se hace uso de las letras minúsculas: p, q, r, s, t,... etc.
Ejemplo:
p = El obrero carga
q = el jefe supervisa
r = el gerente administra
s = todos trabajan
Da clic para seguir el vínculo:
Se simbolizan con el signo: “~” algunos autores lo simbolizan con el signo: "¬"
Negación Simple: es cuando sencillamente se niega una proposición simple.
Ejemplo:
Su simbolización sería: ~p
Se lee: no p
Negación Compuesta: es cuando se niega una proposición compuesta.
Ejemplo:
Su simbolización sería: ~ (p Ʌ q)
Se lee: no es cierto que p y q
Da clic para seguir el vínculo:
es cuando sencillamente se niega una proposición simple.
Ejemplo:
Su simbolización sería: ~p
Se lee: no p
Da clic para seguir el vínculo:
es cuando se niega una proposición compuesta.
Ejemplo:
Su simbolización sería: ~ (p Ʌ q)
Se lee: no es cierto que p y q
Da clic para seguir el vínculo:
(De mayor a menor). Se hace uso de esta jerarquía cuando hay símbolos auxiliares como llaves, corchetes, etc.
1ro: Bi implicador = ↔
2do Disyuntor fuerte = 
3ro Implicador, replicador = → ←
4to Conjuntor y disyuntor débil = v Ʌ
5to Negador = ~
Da clic para seguir el vínculo:
Sirven para determinar cuál es el alcance que tienen los conectores lógicos
Los paréntesis ( )
Los corchetes [ ]
Llaves { }
Da clic para seguir el vínculo:
a. La proposición compuesta conjuntiva es verdadera sólo si las 2 componentes son verdaderas
b. La proposición compuesta conjuntiva es falsa si la primera proposición simple es verdadera y la segunda preposición simple es falsa
c. La proposición compuesta conjuntiva es falsa si la primera proposición simple es falsa y la segunda proposición simples es verdadera
d. La proposición compuesta conjuntiva es falsa si ambas proposiciones simples son falsas
Gráficamente en su tabla de verdad tenemos:
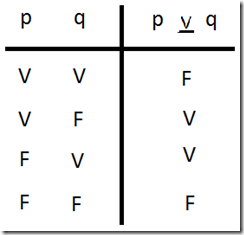
La Disyunción Inclusiva o débil solo es falsa cuando las 2 componentes son falsas; por lo tanto, el resto de casos es verdadero.
a. Si la primera proposición simple es verdadera y la segunda proposición simple es verdadera, entonces, La disyunción como un todo es verdadera.
b. Si la primera proposición simple es falsa y la segunda proposición simple es verdadera, entonces, La disyunción es verdadera.
c. Si la primera proposición simple es verdadera y la segunda proposición simple es falsa, entonces, La disyunción es verdadera.
d. Si la primera proposición simple es falsa y la segunda proposición simple es falsa, entonces, La disyunción como un todo es falsa.
Gráficamente en su tabla de verdad tenemos:
El valor de verdad es falso solamente cuando ambas proposiciones simples son verdaderas o son falsas.
a. Cuando la primera proposición simple es verdadera y la segunda proposición simple es verdadera, la disyunción exclusiva o fuerte es falsa.
b. Cuando la primera proposición simple es falsa y la segunda proposición simple es verdadera, la disyunción exclusiva o fuerte es verdadera.
c. Cuando la primera proposición simple es verdadera y la segunda proposición simple es falsa, la disyunción exclusiva o fuerte es verdadera.
d. Cuando la primera proposición simple es falsa y la segunda proposición simple es falsa, la disyunción exclusiva o fuerte es falsa.
Su tabla de verdad es:
El valor de verdad es falso solamente cuando ambas proposiciones simples son verdaderas o son falsas.
a. Cuando la primera proposición simple es verdadera y la segunda proposición simple es verdadera, la disyunción exclusiva o fuerte es falsa.
b. Cuando la primera proposición simple es falsa y la segunda proposición simple es verdadera, la disyunción exclusiva o fuerte es verdadera.
c. Cuando la primera proposición simple es verdadera y la segunda proposición simple es falsa, la disyunción exclusiva o fuerte es verdadera.
d. Cuando la primera proposición simple es falsa y la segunda proposición simple es falsa, la disyunción exclusiva o fuerte es falsa.
Su tabla de verdad es:
En una tabla de verdad de la condicional, la expresión es falsa cuando la primera proposición simples es verdadera y la segunda proposición simples es falsa.
a. Cuando la primera proposición simples es verdadera y la segunda proposición simple es verdadera, la proposición condicional es verdadera.
b. Cuando la primera proposición simples es verdadera y la segunda proposición simple es falsa, la proposición condicional es falsa.
c. Cuando la primera proposición simples es falsa y la segunda proposición simple es verdadera, la proposición condicional es verdadera.
d. Cuando la primera proposición simples es falsa y la segunda proposición simple es falsa, la proposición condicional es verdadera.
Su tabla de verdad es:
La proposición bicondicional solamente es verdadera cuando las proposiciones simples componentes tienen el mismo valor de verdad, es decir, ambas son verdaderas o ambas son falsas.
a. Cuando la primera proposición simple es verdadera y la segunda proposición simple es verdadera, la proposición bicondicional es verdadera.
b. Cuando la primera proposición simple es verdadera y la segunda proposición simple es falsa, la proposición bicondicional es falsa.
c. Cuando la primera proposición simple es falsa y la segunda proposición simple es verdadera, la proposición bicondicional es falsa.
d. Cuando la primera proposición simple es falsa y la segunda proposición simple es falsa, la proposición bicondicional es verdadera.
Su tabla de verdad es:
La negación invierte los valores de verdad de la proposición simple o compuesta, de tal manera que si su valor es verdadero, lo convierte en falso; y si su valor es falso, lo convierte inmediatamente en verdadero.
Su tabla de verdad es:
Cuando en el desarrollo final de una tabla de verdad todos sus valores si verdaderos (V), estamos frente a un esquema Tautológico ( T ), cuando en el desarrollo final, todos los valores son falsos (F), es un esquema Contradictorio ( ± ) y cuando los valores de un esquema son verdaderos (V) y falsos (F) se llama Contingente o Consistente ( Q ).
TAUTOLOGÍA = TODOS VERDADEROS.
CONTRADICCIÓN = TODOS FALSOS.
CONTINGENTE = VERDADEROS Y FALSOS.
Son también conocidos como operadores, conectores o constantes lógicas, son aquellos que sirven de enlace, conectan o unen 2 proposiciones para formar nuevas proposiciones compuestas, y son:
Da clic para seguir el vínculo:
CONECTIVOS LÓGICOS PARA LA CONJUNCIÓN
CONECTIVOS LÓGICOS PARA LA DISYUNCIÓN INCLUSIVA
CONECTIVOS LÓGICOS PARA LA DISYUNCIÓN EXCLUSIVA
CONECTIVOS LÓGICOS PARA LA CONDICIONAL
CONECTIVOS LÓGICOS PARA LA BICONDICIONAL
CONECTIVOS LÓGICOS PARA LA NEGACIÓN
Su símbolo es "↔", algunos autores utilizan: "≡"
Su simbolización sería: p ↔ q
Se lee: p sí y sólo si q
Su símbolo es "→", algunos autores utilizan: ⊃
Su simbolización sería: p → q
Se lee: si p entonces q
Su símbolo es "
Su simbolización sería: p q
Se lee: o p o q
Su símbolo es V.
Su simbolización sería: p v q
Se lee: p o q
Su símbolo es "Ʌ", aunque algunos autores utilizan el siguiente: "•"
Su simbolización sería: p Ʌ q
Se lee: p y q
Por su calidad las proposiciones pueden ser afirmativas o negativas.
1.- Afirmativas - Enuncian afirmativamente una característica del objeto - sujeto. Ejemplo:
2.-Negativas. - Cuando se rechaza o niega una característica del objeto - sujeto. Ejemplo:
Según la cantidad, las propiedades de las proposiciones pueden ser Universales y particulares.
1.- Universales.- Cuando el sujeto está en toda su extensión; o el predicado se atribuye a toda la extensión del sujeto.
Ejemplo:
Ningún molusco es reptil.
Todo felino es mamífero.
2.- Particulares.- Cuando el sujeto es considerado en parte de su extensión, o el predicado se atribuye una parte de la extensión del sujeto.
Ejemplo:
Algún ave es mamífero.
Algunos hombres son rebeldes.
Son las que no poseen conectores lógicos, son de tipo monario o binario, y son indivisibles, es decir no se pueden separar en dos proposiciones.
Ejemplo:
Todos los empresarios son administradores.
Las proposiciones simples pueden ser:
a. Predicativas.- Son aquellas proposiciones simples que atribuyen o afirman una cualidad o circunstancia de un objeto o sujeto. Ejemplo:
b. Relaciónales.- Son aquellas proposiciones simples que constituyen una relación o enlace entre 2 sujetos u objetos. Ejemplo:
En este caso, A y B son letras que simbolizan a los sujetos y, r indica la relación que se establece ellos.
